1791. Find Center of Star Graph (Leetcode)

There is an undirected star graph consisting of n nodes labeled from 1 to n. A star graph is a graph where there is one center node and exactly n - 1 edges that connect the center node with every other node.

You are given a 2D integer array edges where each edges[i] = [ui, vi] indicates that there is an edge between the nodes ui and vi. Return the center of the given star graph.

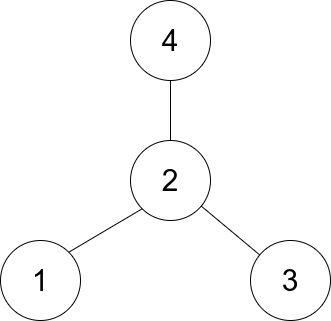
Example: 1

Input: edges = [[1,2],[2,3],[4,2]]

Output: 2

Explanation: As shown in the figure above, node 2 is connected to every other node, so 2 is the center.

Example: 2

Input: edges = [[1,2],[5,1],[1,3],[1,4]]

Output: 1

Constraints:
  • 3 <= n <= 10 ^ 5
  • edges.length == n - 1
  • edges[i].length == 2
  • 1 <= ui, vi <= n
  • ui != vi
  • The given edges represent a valid star graph.
Solution Explanation:
  • First observation that can be made for this problem is that when an edge (u, v) is added, the degree of u as well as v increases by 1.
  • But since it is guaranteed that the graph will be a star graph, we can clearly see that the center node of graph will have maximum degree (since the center node will be called over and over again by other n - 1 nodes while creating edges).
  • So our problem can also be defined as - Find the node with maximum degree in a graph.
Solution Code (Java): class Solution { public int findCenter(int[][] edges) { HashMap<Integer, Integer> map = new HashMap<>(); // incrementing u and v count to calculate degrees for(int[] a : edges) { map.put(a[0], map.getOrDefault(a[0], 0) + 1); map.put(a[1], map.getOrDefault(a[1], 0) + 1); } // the center node will have max degree (i.e degree > 1) // this is because all other nodes will be having degree equal to 1 int ans = -1; for(int key : map.keySet()) { if(map.get(key) > 1) { ans = key; break; } } return ans; } }

Comments

Post a Comment

If you have any queries or need solution for any problem, please let me know.

Popular posts from this blog

123. Best Time to Buy and Sell Stock III

Blog You are given an array prices where prices[i] is the price of a given stock on the i th day. Find the maximum profit you can achieve. You may complete at most two transactions . Note: You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again). Example: 1 Input: prices = [3,3,5,0,0,3,1,4] Output: 6 Example: 2 Input: [1,2,3,4,5] Output: 4 Example: 3 Input: [7,6,4,3,1] Output: 0 Example: 4 Input: [1] Output: 0 Constraints:
Read more

1819. Number of Different Subsequences GCDs (Leetcode)

Blog You are given an array nums that consists of positive integers. The GCD of a sequence of numbers is defined as the greatest integer that divides all the numbers in the sequence evenly. For example, the GCD of the sequence [4,6,16] is 2 . A subsequence of an array is a sequence that can be formed by removing some elements (possibly none) of the array. For example, [2,5,10] is a subsequence of [1,2,1,2,4,1,5,10] . Return the number of different GCDs among all non-empty subsequences of nums . Example: 1 Input: nums = [6,10,3] Output: 5 Example: 2 Input: nums = [5,15,40,5,6] Output: 7
Read more

1799. Maximize Score After N Operations (Leetcode)

Blog You are given nums , an array of positive integers of size 2 * n . You must perform n operations on this array. In the i th operation (1-indexed) , you will: Choose two elements, x and y . Receive a score of i * gcd(x, y) . Remove x and y from nums . Return the maximum score you can receive after performing n operations. The function gcd(x, y) is the greatest common divisor of x and y . Example: 1 Input: nums = [1,2] Output: 1 Example: 2 Input: nums = [3,4,6,8] Output: 11 Example: 3 Input: nums = [1,2,3,4,5,6] Output:
Read more